import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
# Generamos un conjunto de datos desbalanceado
X, y = make_classification(n_classes=2, class_sep=2,
weights=[0.1, 0.90], n_informative=3, n_redundant=1, flip_y=0,
n_features=20, n_clusters_per_class=1, n_samples=1000, random_state=10)
# Dividimos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)8 Práctica avanzada
8.1 Manejo de datos desbalanceados
El desbalance de clases en los conjuntos de datos es un desafío común en el aprendizaje automático, particularmente en aplicaciones como la detección de fraude, donde las clases de interés suelen estar subrepresentadas. Este desbalance puede sesgar el rendimiento de los modelos hacia la clase mayoritaria, resultando en una pobre clasificación de las instancias de la clase minoritaria.
8.1.1 Solución mediante Pesos Diferenciales en SVM
El SVM (Support Vector Machine) con margen blando permite manejar el desbalance mediante la asignación de un costo diferente a las clasificaciones erróneas de las clases. Matemáticamente, esto se refleja en la función de pérdida, donde el costo CC se ajusta por clase:
\[\begin{equation*} L(y,f(x))=C_{clase}⋅max(0,1−y⋅f(x))2 \end{equation*}\]
donde \(C_{clase}\) es el peso asignado a la clase, \(y\) es la etiqueta verdadera, y \(f(x)\) es la decisión del modelo.
8.1.1.1 Implementación
Veamos cómo implementar un clasificador SVM que gestiona el desbalance de clases asignando pesos específicos en scikit-learn.
Primero, creemos un conjunto de datos desbalanceado y dividámoslo en conjuntos de entrenamiento y prueba.
Ahora, ajustaremos un modelo SVM considerando el desbalance mediante el uso de pesos de clase:
# Definimos los pesos de las clases para tratar el desbalance
weights = {0: 1000, 1: 1} # Aumentamos el peso de la clase minoritaria
# Creamos el clasificador SVM con los pesos de clase
clf = SVC(kernel='linear', class_weight=weights)
# Entrenamos el modelo
clf.fit(X_train, y_train)
# Evaluamos el modelo
accuracy = clf.score(X_test, y_test)
print(f'Accuracy: {accuracy:.2f}')Accuracy: 0.988.1.2 Solución #2: Submuestreo y Sobremuestreo
Si el algoritmo de aprendizaje no permite la ponderación de clases, existen técnicas de muestreo como el sobremuestreo (oversampling), el submuestreo (undersampling), y la creación de ejemplos sintéticos mediante algoritmos como SMOTE o ADASYN para equilibrar las clases.
SMOTE (Synthetic Minority Over-sampling Technique) es una técnica de sobremuestreo que crea ejemplos sintéticos de la clase minoritaria para equilibrar el conjunto de datos. Veamos cómo aplicarlo usando la biblioteca imbalanced-learn.
import matplotlib.pyplot as plt
from imblearn.over_sampling import SMOTE
from sklearn.metrics import classification_report
# Aplicamos SMOTE al conjunto de entrenamiento
smote = SMOTE(random_state=42)
X_res, y_res = smote.fit_resample(X_train, y_train)
# Entrenamos un nuevo clasificador SVM con los datos sobremuestreados
clf_smote = SVC(kernel='linear')
clf_smote.fit(X_res, y_res)
# Evaluamos el modelo
y_pred = clf_smote.predict(X_test)
print(classification_report(y_test, y_pred)) precision recall f1-score support
0 0.89 0.96 0.93 26
1 1.00 0.99 0.99 224
accuracy 0.98 250
macro avg 0.94 0.97 0.96 250
weighted avg 0.98 0.98 0.98 250
Comparamos el efecto antes y después de aplicar SMOTE:
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=plt.cm.coolwarm, edgecolors='k')
plt.title('Antes de SMOTE')
plt.subplot(1, 2, 2)
plt.scatter(X_res[:, 0], X_res[:, 1], c=y_res, cmap=plt.cm.coolwarm, edgecolors='k')
plt.title('Después de SMOTE')
plt.show()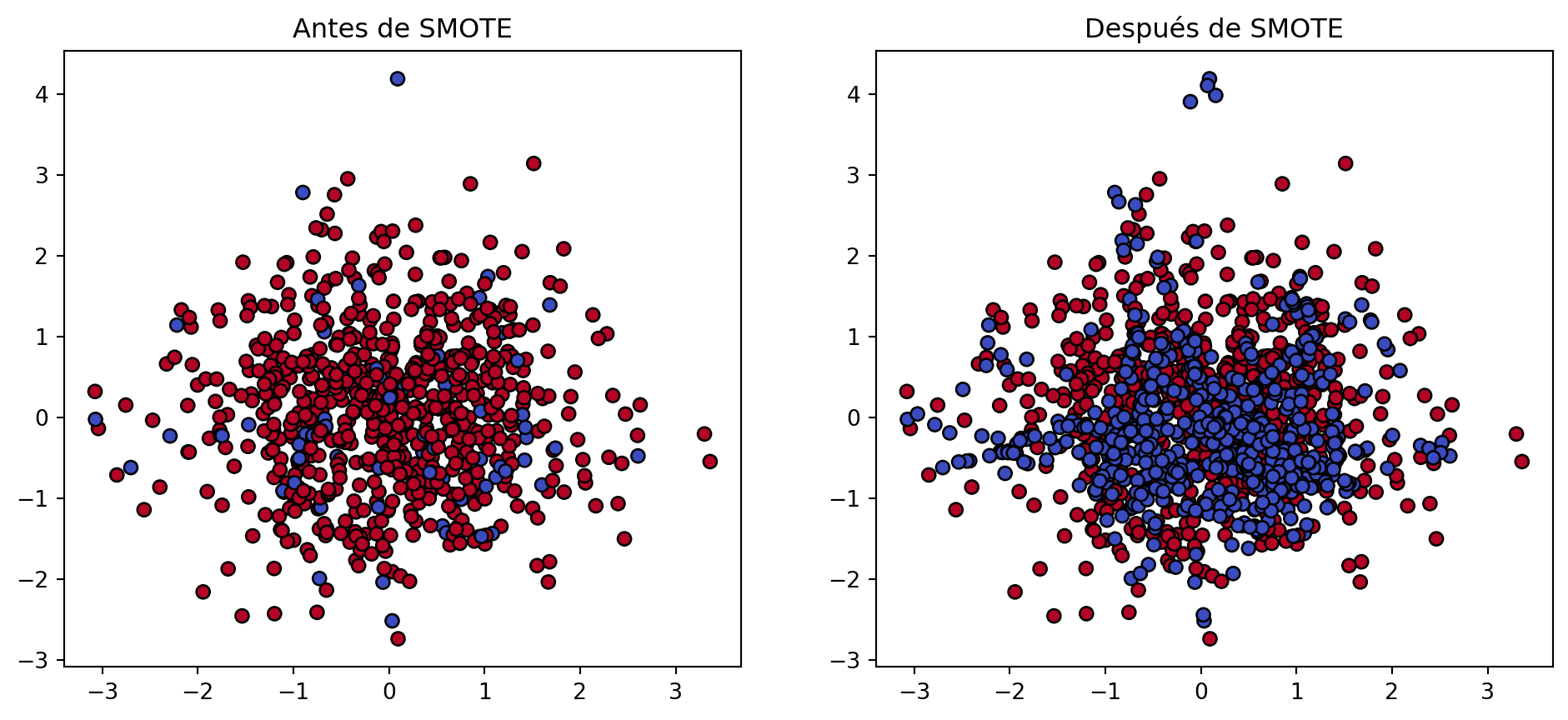
8.2 Combinación de Modelos
La combinación de modelos en el aprendizaje automático es una técnica poderosa que busca mejorar el rendimiento predictivo al integrar las fortalezas de varios modelos. Existen diversas formas de combinar modelos, siendo las más comunes el promedio (averaging), el voto de mayoría (majority vote) y el apilamiento (stacking). Cada uno de estos métodos tiene aplicaciones específicas y beneficios únicos.
8.2.1 Promedio (Averaging)
El método de promedio es aplicable tanto para la regresión como para la clasificación. Consiste en aplicar todos los modelos base al input \(x\) y luego promediar las predicciones. En clasificación, se promedian las probabilidades predichas para cada clase.
Consideremos un conjunto de datos de regresión y combinemos las predicciones de varios modelos de regresión mediante el promedio.
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.linear_model import LinearRegression
import numpy as np
# Generamos un conjunto de datos de regresión
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Entrenamos varios modelos
model_rf = RandomForestRegressor(n_estimators=10, random_state=42).fit(X_train, y_train)
model_gb = GradientBoostingRegressor(n_estimators=10, random_state=42).fit(X_train, y_train)
model_lr = LinearRegression().fit(X_train, y_train)
# Predecimos y promediamos las predicciones
predictions = np.mean([model_rf.predict(X_test), model_gb.predict(X_test), model_lr.predict(X_test)], axis=0)
# Evaluamos el rendimiento del modelo promedio
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_test, predictions)
mse_rf = mean_squared_error(y_test, model_rf.predict(X_test))
mse_gb = mean_squared_error(y_test, model_gb.predict(X_test))
mse_lr = mean_squared_error(y_test, model_lr.predict(X_test))
print(f'MSE del modelo RF: {mse_rf}')
print(f'MSE del modelo GB: {mse_gb}')
print(f'MSE del modelo LR: {mse_lr}')
print(f'MSE del modelo promediado: {mse}')MSE del modelo RF: 9445.970722326663
MSE del modelo GB: 20390.298586678025
MSE del modelo LR: 0.010704979443048707
MSE del modelo promediado: 5842.6963816842568.2.2 Voto de mayoría (Majority Vote)
El voto de mayoría se utiliza para modelos de clasificación. Se aplica cada uno de los modelos base al input xx y se selecciona la clase que obtenga la mayoría de votos entre todas las predicciones.
Utilizaremos varios clasificadores y combinaremos sus predicciones mediante el voto de mayoría.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.metrics import classification_report
# Generamos un conjunto de datos de clasificación
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Entrenamos varios clasificadores
model_rf = RandomForestClassifier(n_estimators=10, random_state=42)
model_lr = LogisticRegression()
model_svc = SVC(probability=True, random_state=42)
# Combinamos mediante voto de mayoría
eclf = VotingClassifier(estimators=[('rf', model_rf), ('lr', model_lr), ('svc', model_svc)], voting='hard')
eclf.fit(X_train, y_train)
model_rf.fit(X_train, y_train)
model_lr.fit(X_train, y_train)
model_svc.fit(X_train, y_train)
# Evaluamos el rendimiento
accuracy = eclf.score(X_test, y_test)
accuracy_rf = model_rf.score(X_test, y_test)
accuracy_lr = model_lr.score(X_test, y_test)
accuracy_svc = model_svc.score(X_test, y_test)
print(f'Accuracy del modelo RF: {accuracy_rf}')
print(f'Accuracy del modelo LR: {accuracy_lr}')
print(f'Accuracy del modelo SVC: {accuracy_svc}')
print(f'Accuracy del modelo combinado mediante voto de mayoría: {accuracy}')
y_pred = eclf.predict(X_test)
print(classification_report(y_test, y_pred))
print(classification_report(y_test, model_rf.predict(X_test)))Accuracy del modelo RF: 0.8333333333333334
Accuracy del modelo LR: 0.85
Accuracy del modelo SVC: 0.8333333333333334
Accuracy del modelo combinado mediante voto de mayoría: 0.8433333333333334
precision recall f1-score support
0 0.81 0.88 0.84 145
1 0.88 0.81 0.84 155
accuracy 0.84 300
macro avg 0.84 0.84 0.84 300
weighted avg 0.85 0.84 0.84 300
precision recall f1-score support
0 0.80 0.88 0.84 145
1 0.88 0.79 0.83 155
accuracy 0.83 300
macro avg 0.84 0.83 0.83 300
weighted avg 0.84 0.83 0.83 300
8.2.3 Apilamiento (Stacking)
El apilamiento consiste en combinar varios modelos base y utilizar sus salidas como input para un meta-modelo, que hace la predicción final. Ejemplo en Python para Stacking
Implementaremos stacking con varios modelos base y un meta-modelo de regresión logística.
from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
# Definimos los modelos base y el meta-modelo
base_models = [('rf', RandomForestClassifier(n_estimators=10, random_state=42)),
('svc', SVC(probability=True, random_state=42))]
meta_model = LogisticRegression()
# Creamos el modelo de apilamiento
stacking_model = StackingClassifier(estimators=base_models, final_estimator=meta_model)
# Entrenamos y evaluamos el modelo de apilamiento
stacking_model.fit(X_train, y_train)
accuracy = stacking_model.score(X_test, y_test)
print(f'Accuracy del modelo de apilamiento: {accuracy}')
print(classification_report(y_test, stacking_model.predict(X_test)))
print(classification_report(y_test, model_rf.predict(X_test)))
print(classification_report(y_test, model_svc.predict(X_test)))Accuracy del modelo de apilamiento: 0.84
precision recall f1-score support
0 0.82 0.86 0.84 145
1 0.86 0.82 0.84 155
accuracy 0.84 300
macro avg 0.84 0.84 0.84 300
weighted avg 0.84 0.84 0.84 300
precision recall f1-score support
0 0.80 0.88 0.84 145
1 0.88 0.79 0.83 155
accuracy 0.83 300
macro avg 0.84 0.83 0.83 300
weighted avg 0.84 0.83 0.83 300
precision recall f1-score support
0 0.81 0.86 0.83 145
1 0.86 0.81 0.83 155
accuracy 0.83 300
macro avg 0.83 0.83 0.83 300
weighted avg 0.83 0.83 0.83 300
8.3 Entrenamiento de Redes Neuronales
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# Crear un generador de datos con normalización
datagen = ImageDataGenerator(rescale=1./255)
# Suponiendo que 'directorio_de_datos' es el camino a las imágenes
train_generator = datagen.flow_from_directory(
directorio_de_datos,
target_size=(200, 200), # Todas las imágenes se redimensionan a 200x200
batch_size=32,
class_mode='binary' # o 'categorical' para clasificación multiclase
)
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
# Crear un tokenizador para convertir palabras a índices
tokenizer = Tokenizer(num_words=10000) # Considera las 10,000 palabras más comunes
tokenizer.fit_on_texts(textos) # 'textos' es una lista de documentos de texto
# Convertir textos en secuencias de índices
sequences = tokenizer.texts_to_sequences(textos)
# Acolchar secuencias para que tengan la misma longitud
data = pad_sequences(sequences, maxlen=100) # Longitud fija de 100 para todas las secuencias
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
# Crear un modelo simple como punto de partida
model = Sequential([
Dense(64, activation='relu', input_shape=(100,)), # Ejemplo para datos vectorizados de longitud 100
Dropout(0.5), # Regularización mediante Dropout
Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
# Entrenar el modelo
model.fit(data, etiquetas, epochs=10, validation_split=0.2) # 'etiquetas' es un array de etiquetas