4 Anatomía de un algoritmo de aprendizaje

4.1 Bloques de construcción de un algoritmo de aprendizaje

En los algoritmos de aprendizaje que abarcamos en la sección anterior podemos observar los 3 bloques que se utilizan para construirlos:

Bloques de un algoritmo de aprendizaje.
Bloque	Descripción
Función de pérdida	Método para evaluar que tan bien se ajusta el modelo a los datos de entrenamiento Si el modelo no predice adecuadamente, la función de pérdida da un resultado mayor
Criterio de optimización	Debe estar basado en la función de pérdida
Rutina de optimización	Utiliza los valores de la función objetivo y los datos para ajustar los parámetros del modelo

4.2 Descenso de gradiente (GD)

El descenso de gradiente es un algoritmo iterativo que permite encontrar el máximo o mínimo de una función dada, y se utiliza en los algoritmos de machine learning (ML) y deep learning (DL) para minimizar las funiciones de pérdida.

En conjunto con el descenso de gradiente estocástico, son de los algoritmos más utilizados en ML y DL.

4.2.1 Requisitos de la función a optimizar

Diferenciable: tiene una derivada para cada punto en su dominio.

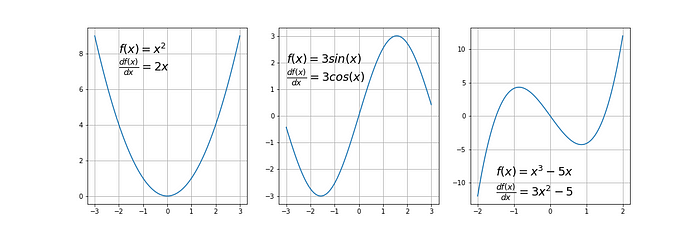
Funciones diferenciables. — Funciones diferenciables

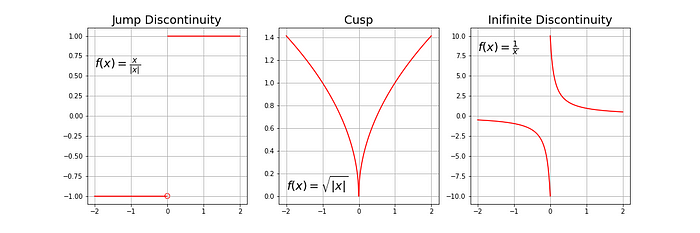
Funciones no diferenciables. — Funciones no diferenciables

Convexa: para una función univariada, una línea que conecta dos puntos de la función pasa sobre o encima de la función. Las funciones convexas solo tienen un mínimo, que es el mínimo global.

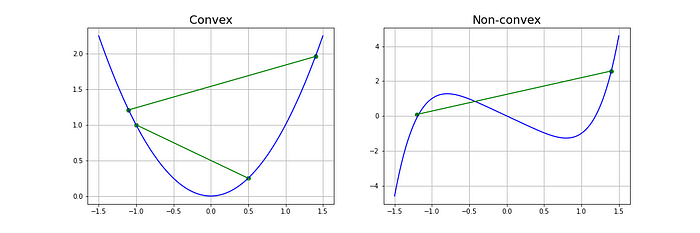
Funciones convexas. — Funciones convexas

Los criterios de optimización de muchos modelos (regresión lineal y logística, SVM, entre otros) son convexos, por lo que el GD es un método adecuado.

Los criterios de optimización para las redes neuronales no son convexos (tienen mínimos locales y globales), pero en la práctica es suficiente encontrar mínimos globales, por lo que el GD también resulta un método útil.

4.2.2 Gradiente

Es la pendiente de una curva en una dirección específica.

En funciones univariadas la obtenemos evaluando la primera derivada en un punto de interés.

En funciones multivariadas, es un vector de derivadas en cada dirección principal, lo que conocemos como derivadas parciales.

El gradiente para una función \(f(x)\) en un punto \(p\) está dado por: \[ \nabla f(p) = \begin{bmatrix} \frac{\partial f}{\partial x_1} (p) \\ \vdots \\ \frac{\partial f}{\partial x_n} (p) \end{bmatrix} \]

4.2.3 Algoritmo de descenso de gradiente

El método se puede resumir mediante la siguiente ecuación:

\[ p_{n+1} = p_n - \alpha \nabla f(p_n) \]

Paso a paso:

Escoger un punto inicial: \(p_n\)
Calcular el gradiente en este punto: \(\nabla f(p_n)\)
Moverse en la dirección contraria al gradiente, a una distancia dada por la tasa de aprendizaje \(\alpha\)
Repetir pasos 2 y 3 hasta que se cumpla lo siguiente:

Número máximo de iteraciones alcanzado
El tamaño del paso es más pequeño que la tolerancia definida (cambio en \(\alpha\) o gradiente muy baja)

4.2.4 Imports

import matplotlib.pyplot as plt
import numpy as np

from typing import Callable

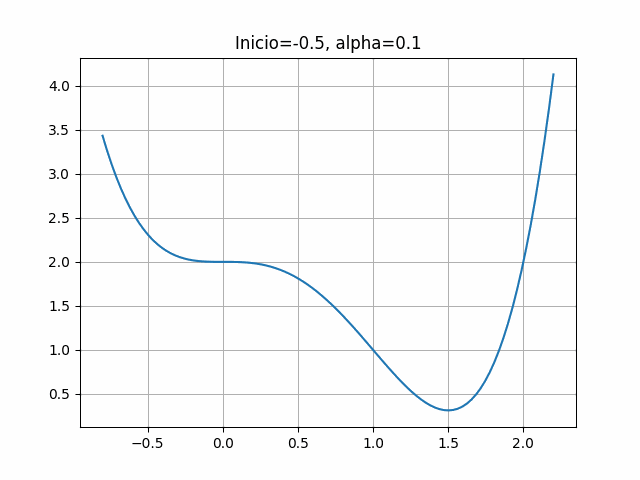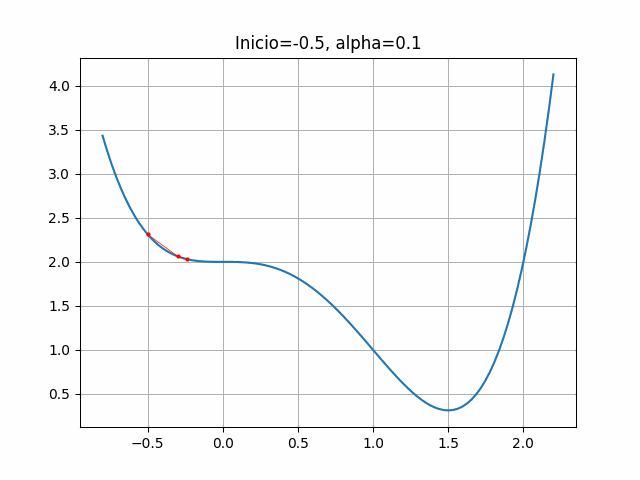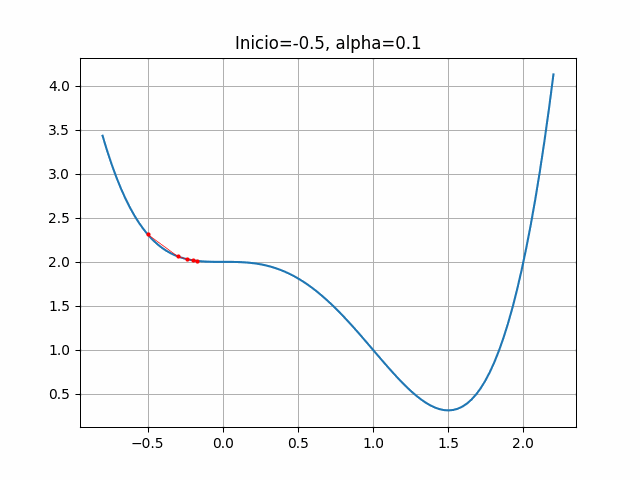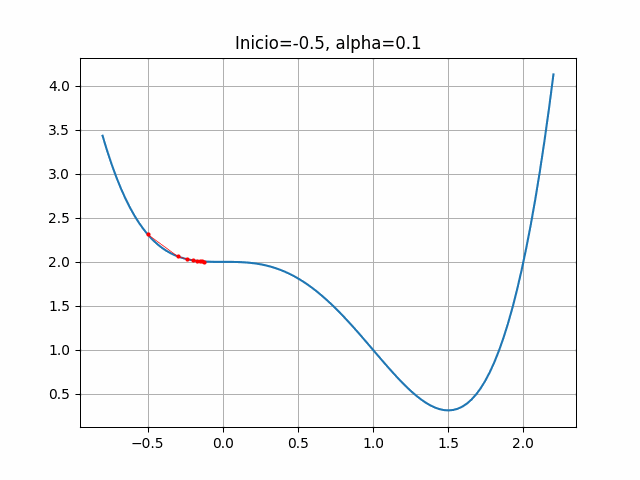
4.2.5 Ejemplo 1: función univariada, derivable no convexa

Función a optimizar: \[\begin{equation*} f(x) = x^4 - 2x^3 + 2 \end{equation*}\] Y su gradiente:

\[\begin{equation*} \frac{df(x)}{dx} = 4x^3-6x^2 \end{equation*}\]

Definiendo \(f(x)\) y \(\frac{df(x)}{dx}\) en python

# f(x)
def f_ej1(x:float):
  return x**4-2*x**3+2

# df(x)/dx
def dfdx_ej1(x:float):
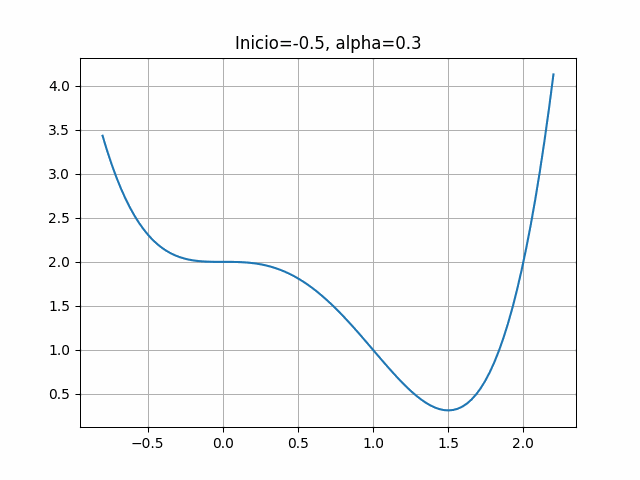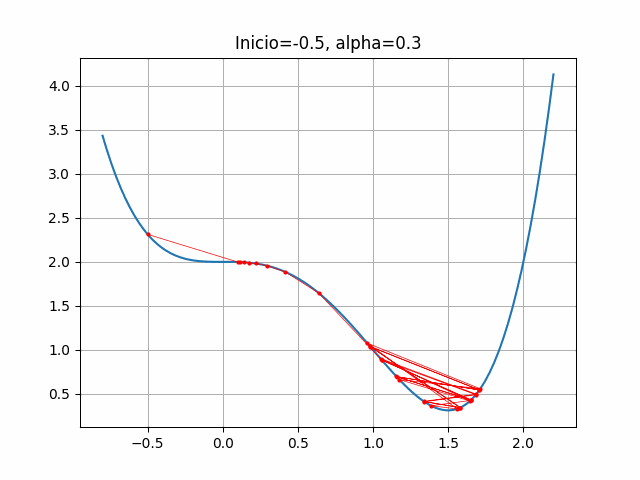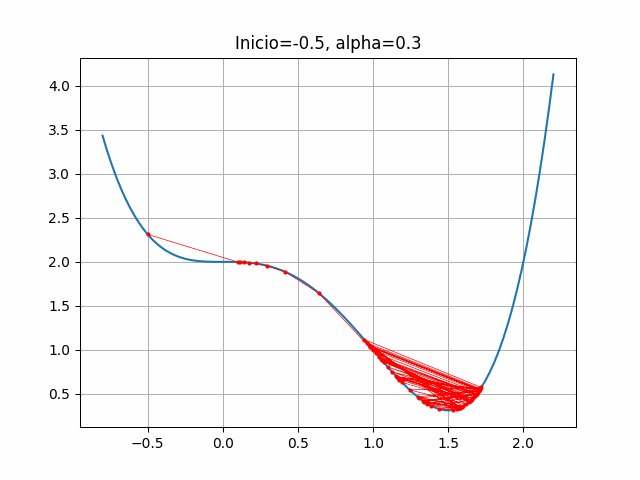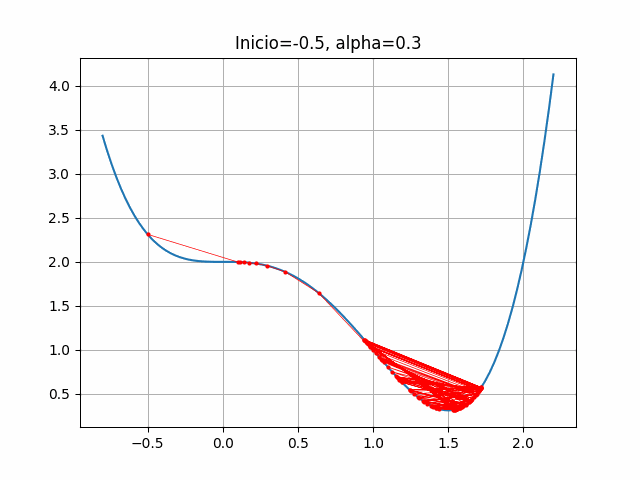
  return 4*x**3-6*x**2

4.2.6 Gráfica de \(f(x)\)

x = np.linspace(-0.8, 2.2, 100)
y = f_ej1(x)
plt.grid(True)

plt.plot(x,y)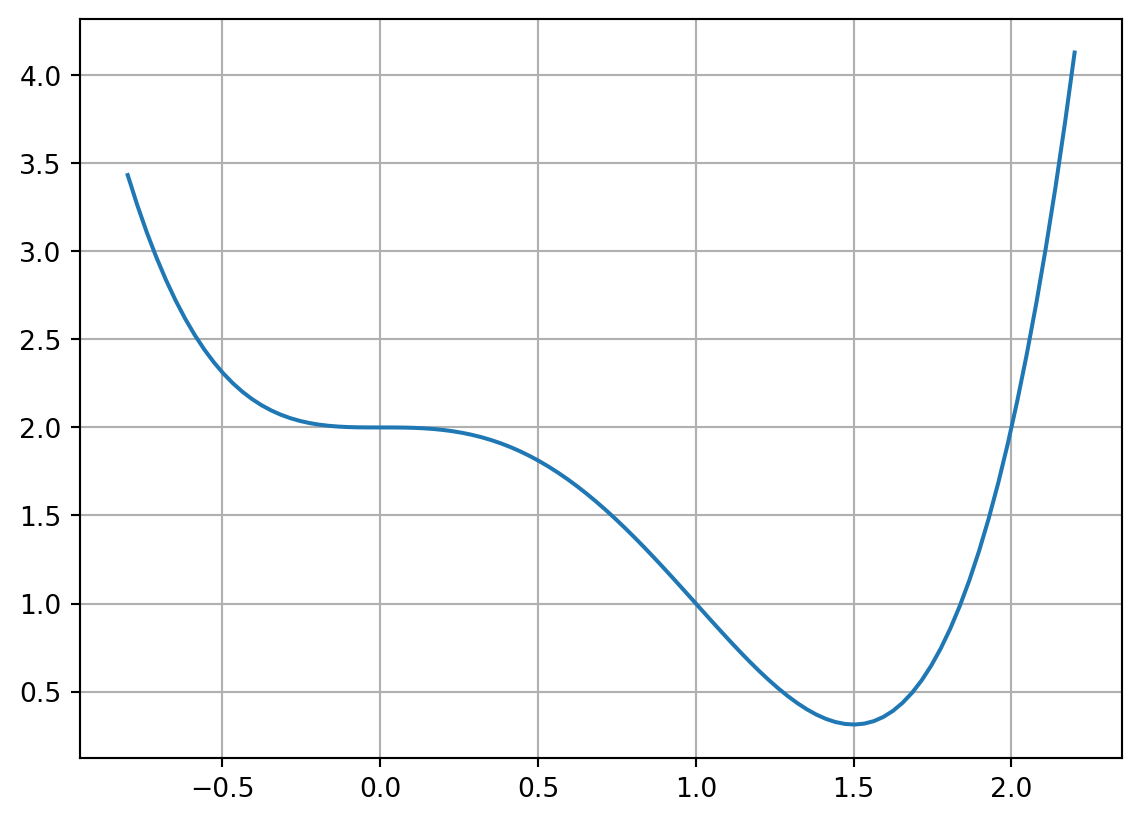

Definiendo algoritmo gradient_descent

def gradient_descent(start: float, gradient: Callable[[float], float],
                     learn_rate: float, max_iter: int, tol: float = 0.01):
    x = start
    steps = [start]  # history tracking

    for _ in range(max_iter):
        diff = learn_rate*gradient(x)
        if np.abs(diff) < tol:
            break
        x = x - diff
        steps.append(x)  # history tracing
  
    return steps, x

Llamando a gradient_descent para el ejemplo 1

start = 2
gradient = dfdx_ej1
learn_rate = 0.1
max_iter = 100

gradient_descent(start, gradient, learn_rate, max_iter)

([2, 1.2, 1.3728000000000002, 1.4686874222592001, 1.4957044497076786],
 1.4957044497076786)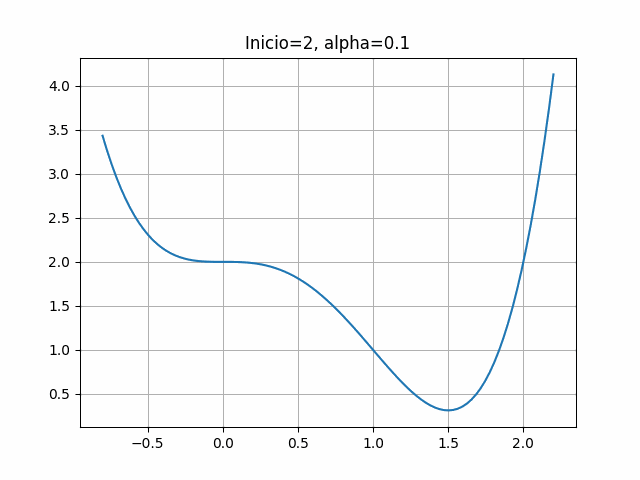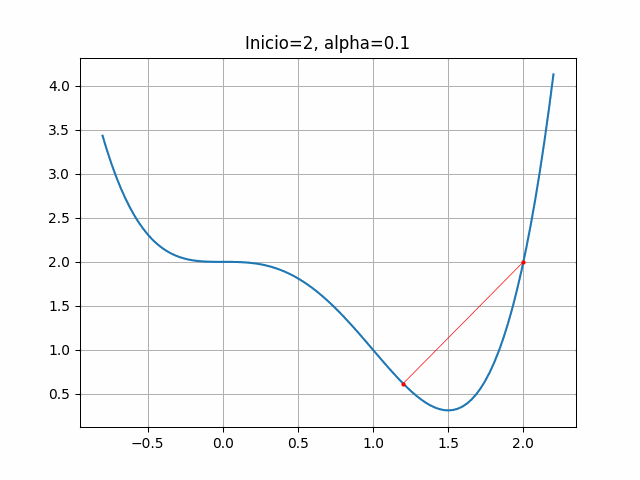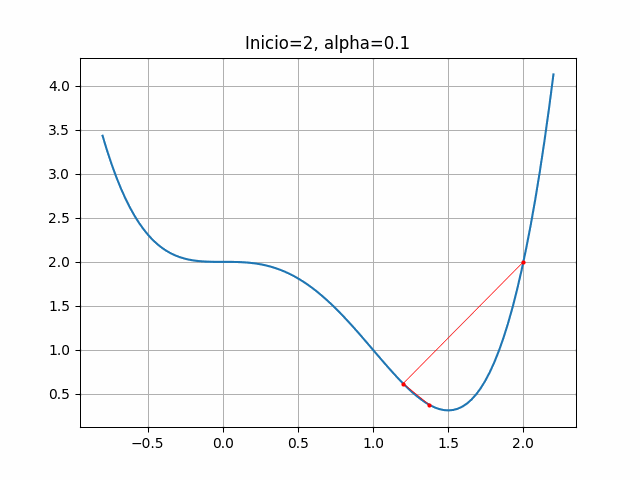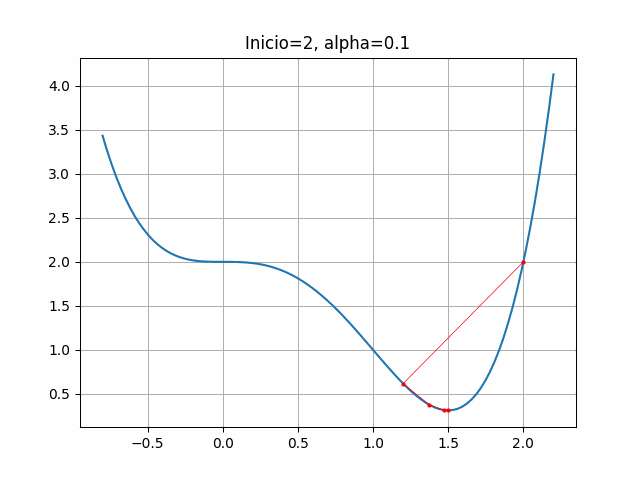

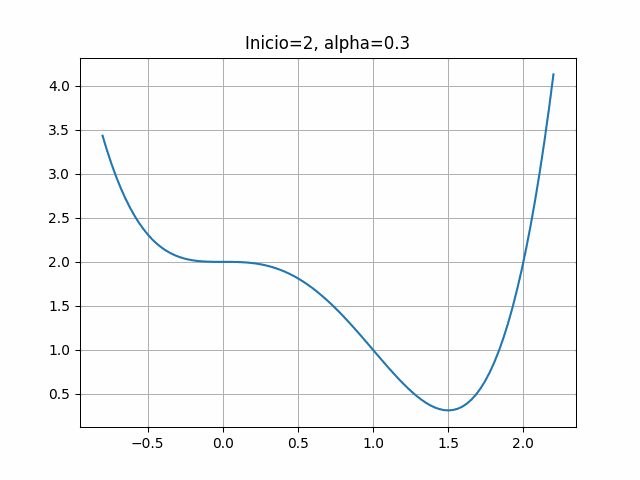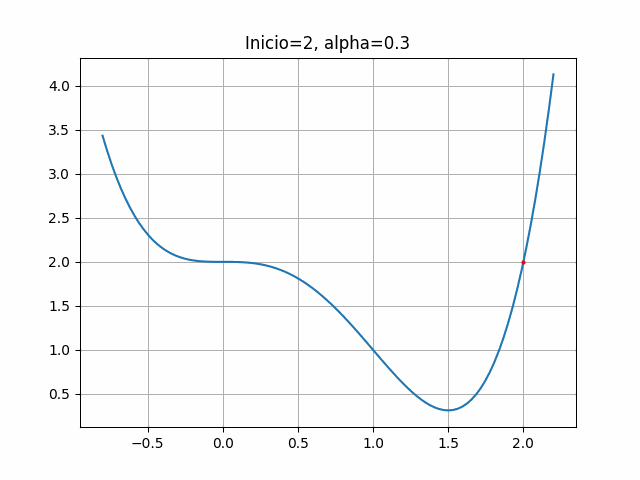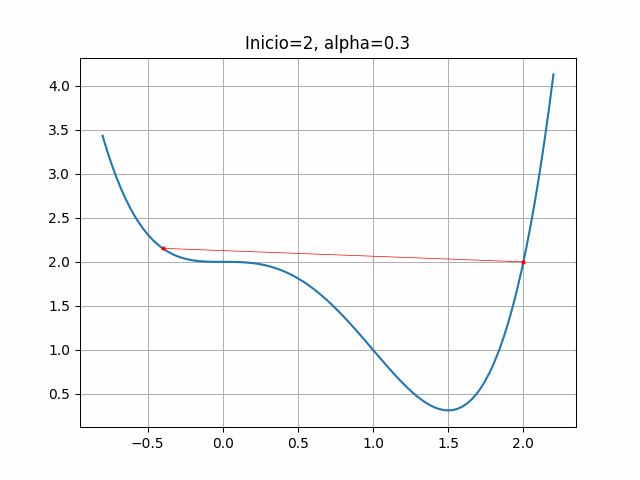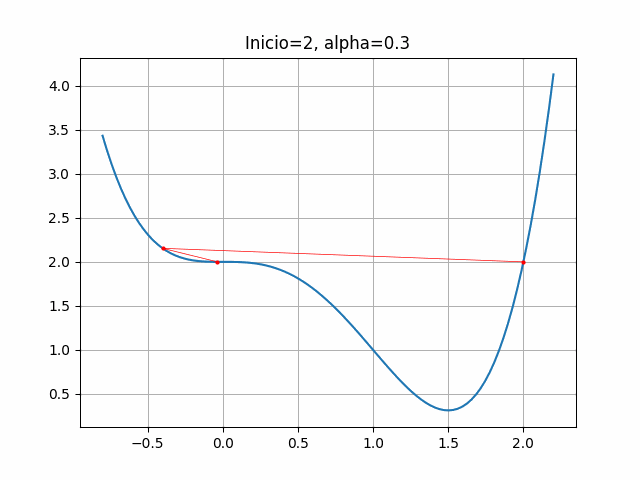
Variaciones al ejemplo 1

Figura 4.2: Animación del ejemplo 1 (variación 1).

Figura 4.3: Animación del ejemplo 1 (variación 2).

Figura 4.4: Animación del ejemplo 1 (variación 3).

4.2.7 Códigos usados para esta sección

# Gradient Descent
# gcorazzari

import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np

from typing import Callable


def update(frame):
    x = x_gd[:frame]
    y = y_gd[:frame]
    line_gd.set_xdata(x)
    line_gd.set_ydata(y)
    return line_gd


def gradient_descent(
    start: float,
    gradient: Callable[[float], float],
    learn_rate: float,
    max_iter: int,
    tol: float = 0.01,
):
    x = start
    steps = [start]  # history tracking

    for _ in range(max_iter):
        diff = learn_rate * gradient(x)
        if np.abs(diff) < tol:
            break
        x = x - diff
        steps.append(x)  # history tracing

    return steps, x


# EJ1-4
def f_ej1(x: float):
    return x**4 - 2 * x**3 + 2


def dfdx_ej1(x: float):
    return 4 * x**3 - 6 * x**2


start = -0.5
gradient = dfdx_ej1
learn_rate = 0.3
max_iter = 100

res_ej1 = gradient_descent(start, gradient, learn_rate, max_iter)

fig, ax = plt.subplots()

x = np.linspace(-0.8, 2.2, 100)
y = f_ej1(x)

line = ax.plot(x, y)

x_gd = np.array(res_ej1[0])
y_gd = f_ej1(x_gd)

line_gd = ax.plot(
    res_ej1[0][0], f_ej1(res_ej1[0][0]), "ro-", linewidth=0.5, markersize=2
)[0]

ani = animation.FuncAnimation(fig=fig, func=update, frames=102, interval=200)

plt.grid(True)
plt.title("Inicio=-0.5, alpha=0.3")

writer = animation.PillowWriter(fps=5)

plt.show()
ani.save("ej1-4.gif", writer=writer)


# EJ1-3
def f_ej1(x: float):
    return x**4 - 2 * x**3 + 2


def dfdx_ej1(x: float):
    return 4 * x**3 - 6 * x**2


start = -0.5
gradient = dfdx_ej1
learn_rate = 0.1
max_iter = 100

res_ej1 = gradient_descent(start, gradient, learn_rate, max_iter)

fig, ax = plt.subplots()

x = np.linspace(-0.8, 2.2, 100)
y = f_ej1(x)

line = ax.plot(x, y)

x_gd = np.array(res_ej1[0])
y_gd = f_ej1(x_gd)

line_gd = ax.plot(
    res_ej1[0][0], f_ej1(res_ej1[0][0]), "ro-", linewidth=0.5, markersize=2
)[0]

ani = animation.FuncAnimation(fig=fig, func=update, frames=9, interval=500)

plt.grid(True)
plt.title("Inicio=-0.5, alpha=0.1")

writer = animation.PillowWriter(fps=5)

plt.show()
ani.save("ej1-3.gif", writer=writer)


# EJ1-2
def f_ej1(x: float):
    return x**4 - 2 * x**3 + 2


def dfdx_ej1(x: float):
    return 4 * x**3 - 6 * x**2


start = 2
gradient = dfdx_ej1
learn_rate = 0.3
max_iter = 100

res_ej1 = gradient_descent(start, gradient, learn_rate, max_iter)

fig, ax = plt.subplots()

x = np.linspace(-0.8, 2.2, 100)
y = f_ej1(x)

line = ax.plot(x, y)

x_gd = np.array(res_ej1[0])
y_gd = f_ej1(x_gd)

line_gd = ax.plot(
    res_ej1[0][0], f_ej1(res_ej1[0][0]), "ro-", linewidth=0.5, markersize=2
)[0]

ani = animation.FuncAnimation(fig=fig, func=update, frames=4, interval=200)

plt.grid(True)
plt.title("Inicio=2, alpha=0.3")

writer = animation.PillowWriter(fps=5)

plt.show()
ani.save("ej1-2.gif", writer=writer)


# EJ1-1
def f_ej1(x: float):
    return x**4 - 2 * x**3 + 2


def dfdx_ej1(x: float):
    return 4 * x**3 - 6 * x**2


start = 2
gradient = dfdx_ej1
learn_rate = 0.1
max_iter = 100

res_ej1 = gradient_descent(start, gradient, learn_rate, max_iter)

fig, ax = plt.subplots()

x = np.linspace(-0.8, 2.2, 100)
y = f_ej1(x)

line = ax.plot(x, y)

x_gd = np.array(res_ej1[0])
y_gd = f_ej1(x_gd)

line_gd = ax.plot(
    res_ej1[0][0], f_ej1(res_ej1[0][0]), "ro-", linewidth=0.5, markersize=2
)[0]

ani = animation.FuncAnimation(fig=fig, func=update, frames=6, interval=500)

plt.grid(True)
plt.title("Inicio=2, alpha=0.1")

writer = animation.PillowWriter(fps=5)

plt.show()
ani.save("ej1-1.gif", writer=writer)