from sklearn import datasets
from sklearn.model_selection import train_test_split
digits = datasets.load_digits()
n_samples = len(digits.images)
X = digits.images.reshape((n_samples, -1))
y = digits.target == 8
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)5 Capítulo 5
5.1 5.2:Selección de algoritmos
Elegir un algoritmo puede ser una tarea difícil. En el caso de que se disponga de mucho tiempo se pueden probar varios, sin embargo no siempre es el caso, por lo que hay una serie de preguntas que se pueden realizar con el fin de hacer el proceso más eficiente.
5.1.1 Explicabilidad o interpretabilidad
Con que facilidad el algoritmo logra explicar las predicciones que realiza, por lo general un modelo que realiza una predicción específica es dificíl de entender y aún más de explicar. Algunos ejemplos son los modelos de redes neuronales o el método de emsamble. Estos algoritmos que carecen de tal explicación se llaman algoritmo de caja negra.Por otro lado, los algoritmos de aprendizaje kNN, regresión lineal o árbol de decisión producen modelos que no siempre son los más precisos, sin embargo, la forma en que hacen su predicción es muy sencilla.
Ejemplo

5.1.2 Requisitos de memoria
Si el conjunto de datos se puede cargar de forma completa en la memoria RAM del servidor o computador, entonces la disponibilidad de logaritmos es amplia. Sin embargo, si ese no es el caso, se debe optar por logaritmos de aprendizaje incremental, estos pueden mejorar el modelo añadiendo más datos gradualmente, básicamente se adaptan a nuevos nuevos sin el olvidar la información ya existente.
5.1.3 Número de funciones y característica
Algunos algoritmos, como las redes neuronales y el descenso de gradiente, pueden manejar un gran número de ejemplos y millones de características. Otros, como SVM, pueden ser muy modestos en su capacidad. Entonces, a la hora de escoger un logaritmo se debe considerar el tamaño de los datos y la cantidad de funciones.
5.1.4 Características categóricas frente a numéricas
Algunos algoritmos solo pueden funcionar con datos numéricos, por lo que si se tienen datos en un formato categórico o no numérico, se deberá considerar un proceso para convertirlos en datos numéricos mediante técnicas como la codificación one-hot.
5.1.5 linealidad de los datos
Si los datos son linealmente separables o pueden modelarse mediante un modelo lineal, se puede utilizar SVM, regresión logística o la regresión lineal, si no es el caso las redes neuronales o los algoritmos de conjunto, son una mejor opción.
Ejemplo
5.1.6 Velocidad de entrenamiento
Es el tiempo que tarda un algoritmo en aprender y crear un modelo. Las redes neuronales son conocidas por la considerable cantidad de tiempo que requieren para entrenar un modelo. Los algoritmos de máquina tradicionales como K-Vecinos más cercanos y Regresión logística toman mucho menos tiempo. Algunos algoritmos, como Bosque aleatorio, requieren diferentes tiempos de entrenamiento según los núcleos de CPU que se utilizan.
Ejemplo
5.1.7 Velocidad de predicción
Tiempo que le toma a un modelo hacer sus predicciones, en este caso se debe considerar qué tan rápido debe ser el modelo a la hora de generar predicciones y para que función se está utilizando el modelo escogido. Si no se quiere adivinar cuál es el mejor algoritmo para los datos, una forma de elegir es utilizar la prueba de validación.
Ejemplo

5.2 5.3:Three sets
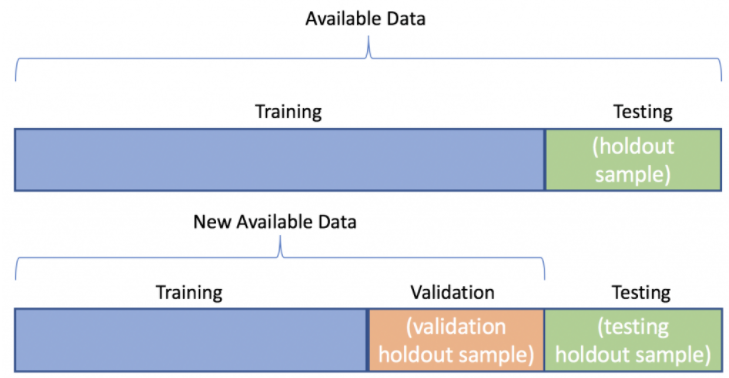
En Machine Learning, para el estudio y construcción de algoritmos que sean capaces de aprender de los datos y hacer predicciones utilizando esa información, se utiliza la construcción de un modelo matemático a partir de datos de entrada y estos datos para ser utilizados se dividen en conjuntos de datos, estos son:
- Conjunto de entrenamiento
- Conjunto de validación
- Conjunto de prueba
El conjunto de entrenamiento, suele ser el conjunto más grande y es el que se utiliza para construir el modelo, los conjuntos de validación y prueba suelen tener el mismo tamaño y esto son menores que en el conjunto de entrenamiento , tanto los conjuntos de validación y prueba no son usados para construir el modelo. A estos conjuntos se les suele llamar conjuntos esfera.
Ejemplo
6 Ajuste de hiperparámetros
El analista de datos debe seleccionar buenos hiperparámetros para el algoritmo que se esté trabajando. Como se sabe que lkos hiperparámetros no son optimizados por el algoritmo de aprendizaje por si solo; el analista debe ajustar la mejor combinación de hiperparámetros.
Una forma usual de realizar esto es, si se tienen suficientes datos para tener un conjunto de validación decente (cada calse tiene al menos un par de docenas de ejemplos) y el número de hiperparámetros y sus rangos no son muy grandes; se puede utilizar grid search. Este método es la más simple estrategia para ajustar los hiperparámetros.
Asuma que entrenamos un SVM y queremos ajustar dos hiperparámetros: el parámetro de penalización \(C\) (un número real positivo) y el kernel (si es ‘linear’ o ‘rbf’). Si es la primera vez trabajando con el datset y no tenemos un rango de valores para \(C\), un truco muy común es usar una escala logarítimica; entonces podemos tomar los valores de \([0.001, 0.01, 0.1, 1.0, 10, 100, 1000]\). Note que debido lo anterior tenemos 14 combinaciones de hiperparámetros diferentes: [(0.001, ‘linear’), (0.01, ‘linear’), (0.1, ‘linear’), (1.0, ‘linear’), (10, ‘linear’), (100, ‘linear’), (1000, ‘linear’), (0.001, ‘rbf’), (0.01, ‘rbf’), (0.1, ‘rbf’), (1.0, ‘rbf’), (10, ‘rbf’), (100, ‘rbf’), (1000, ‘rbf’)]
Lo que se hace es tomar el conujunto de entrenamiento y entrenarlo con los 14 modelos diferentes. Luego, se evalúa el rendimiento de cada modelo con los datos de validación usando alguna métrica. Y se elige el que tenga la mejor métrica. Y por último se evalúa con el conjunto de prueba.
Un problema es el consumo de tiempo. Para ello, hay técnicas más eficientes como random search y bayesian hyperparameter optimization.
En el random search, uno le da una una distribución estadística para cada hiperparámetro y el número total de combinaciones que ser quieren realizar. La técnica bayesiana utiliza los resultados anteriores para elegir los próximos valores para evaluar.
6.1 Validación Cruzada
Cuando no se tienen muchos datos para ajustar los hiperparámetros. Entonces, podemos dividir el conjunto de entrenamiento en varios subconjuntos (fold) del mismo tamaño, lo usual es usar 5 folds. Así, se dividen los datos de entrenamiento en 5 folds \(\{F_1, F_2, F_3, F_4, F_5\}\) cada una contiene el \(20\%\) de los datos de entrenamiento. Así, se entrenan 5 modelos, de la siguiente forma: para el primer modelo \(f_1\) se utilizan los folds \(F_2, F_3, F_4, F_5\) y \(F_1\) se utiliza como conjunto de validación; para el segundo modelo \(f_2\) se utilizan los folds \(F_1, F_3, F_4, F_5\) y el \(F_2\) es el conjutno de validación; y aspi hasta completar \(f_5\).
Se puede aplicar grid search con la validación cruzada para encontrar los mejores valores para los hiperparámetro de nuestro modelo.
6.2 Ejemplo
import pandas as pd
def print_dataframe(filtered_cv_results):
"""Pretty print for filtered dataframe"""
for mean_precision, std_precision, mean_recall, std_recall, params in zip(
filtered_cv_results["mean_test_precision"],
filtered_cv_results["std_test_precision"],
filtered_cv_results["mean_test_recall"],
filtered_cv_results["std_test_recall"],
filtered_cv_results["params"],
):
print(
f"precision: {mean_precision:0.3f} (±{std_precision:0.03f}),"
f" recall: {mean_recall:0.3f} (±{std_recall:0.03f}),"
f" for {params}"
)
print()
def refit_strategy(cv_results):
"""Define the strategy to select the best estimator.
The strategy defined here is to filter-out all results below a precision threshold
of 0.98, rank the remaining by recall and keep all models with one standard
deviation of the best by recall. Once these models are selected, we can select the
fastest model to predict.
Parameters
----------
cv_results : dict of numpy (masked) ndarrays
CV results as returned by the `GridSearchCV`.
Returns
-------
best_index : int
The index of the best estimator as it appears in `cv_results`.
"""
# print the info about the grid-search for the different scores
precision_threshold = 0.98
cv_results_ = pd.DataFrame(cv_results)
print("All grid-search results:")
print_dataframe(cv_results_)
# Filter-out all results below the threshold
high_precision_cv_results = cv_results_[
cv_results_["mean_test_precision"] > precision_threshold
]
print(f"Models with a precision higher than {precision_threshold}:")
print_dataframe(high_precision_cv_results)
high_precision_cv_results = high_precision_cv_results[
[
"mean_score_time",
"mean_test_recall",
"std_test_recall",
"mean_test_precision",
"std_test_precision",
"rank_test_recall",
"rank_test_precision",
"params",
]
]
# Select the most performant models in terms of recall
# (within 1 sigma from the best)
best_recall_std = high_precision_cv_results["mean_test_recall"].std()
best_recall = high_precision_cv_results["mean_test_recall"].max()
best_recall_threshold = best_recall - best_recall_std
high_recall_cv_results = high_precision_cv_results[
high_precision_cv_results["mean_test_recall"] > best_recall_threshold
]
print(
"Out of the previously selected high precision models, we keep all the\n"
"the models within one standard deviation of the highest recall model:"
)
print_dataframe(high_recall_cv_results)
# From the best candidates, select the fastest model to predict
fastest_top_recall_high_precision_index = high_recall_cv_results[
"mean_score_time"
].idxmin()
print(
"\nThe selected final model is the fastest to predict out of the previously\n"
"selected subset of best models based on precision and recall.\n"
"Its scoring time is:\n\n"
f"{high_recall_cv_results.loc[fastest_top_recall_high_precision_index]}"
)
return fastest_top_recall_high_precision_indexAhora, se define el grid search
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
scores = ['precision', 'recall']
tuned_params = [
{'kernel':['rbf'], 'gamma':[1e-3, 1e-4], 'C':[1, 10, 100, 1000]},
{'kernel':['linear'], 'C':[1, 10, 100, 1000]}
]
grid_search = GridSearchCV(SVC(), tuned_params, scoring=scores, refit=refit_strategy)
grid_search.fit(X_train, y_train)All grid-search results:
precision: 1.000 (±0.000), recall: 0.854 (±0.063), for {'C': 1, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.257 (±0.061), for {'C': 1, 'gamma': 0.0001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 0.968 (±0.039), recall: 0.780 (±0.083), for {'C': 10, 'gamma': 0.0001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 0.905 (±0.058), recall: 0.889 (±0.074), for {'C': 100, 'gamma': 0.0001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 0.904 (±0.058), recall: 0.890 (±0.073), for {'C': 1000, 'gamma': 0.0001, 'kernel': 'rbf'}
precision: 0.695 (±0.073), recall: 0.743 (±0.065), for {'C': 1, 'kernel': 'linear'}
precision: 0.643 (±0.066), recall: 0.757 (±0.066), for {'C': 10, 'kernel': 'linear'}
precision: 0.611 (±0.028), recall: 0.744 (±0.044), for {'C': 100, 'kernel': 'linear'}
precision: 0.618 (±0.039), recall: 0.744 (±0.044), for {'C': 1000, 'kernel': 'linear'}
Models with a precision higher than 0.98:
precision: 1.000 (±0.000), recall: 0.854 (±0.063), for {'C': 1, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.257 (±0.061), for {'C': 1, 'gamma': 0.0001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}
Out of the previously selected high precision models, we keep all the
the models within one standard deviation of the highest recall model:
precision: 1.000 (±0.000), recall: 0.854 (±0.063), for {'C': 1, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
precision: 1.000 (±0.000), recall: 0.877 (±0.069), for {'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}
The selected final model is the fastest to predict out of the previously
selected subset of best models based on precision and recall.
Its scoring time is:
mean_score_time 0.008416
mean_test_recall 0.877206
std_test_recall 0.069196
mean_test_precision 1.0
std_test_precision 0.0
rank_test_recall 3
rank_test_precision 1
params {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
Name: 2, dtype: objectGridSearchCV(estimator=SVC(),
param_grid=[{'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001],
'kernel': ['rbf']},
{'C': [1, 10, 100, 1000], 'kernel': ['linear']}],
refit=<function refit_strategy at 0x131cf09a0>,
scoring=['precision', 'recall'])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(estimator=SVC(),
param_grid=[{'C': [1, 10, 100, 1000], 'gamma': [0.001, 0.0001],
'kernel': ['rbf']},
{'C': [1, 10, 100, 1000], 'kernel': ['linear']}],
refit=<function refit_strategy at 0x131cf09a0>,
scoring=['precision', 'recall'])SVC()
SVC()